half range fourier series

By Coa_754Travis 01 Sep, 2022 Post a Comment

Fast Fourier Transform FFT can perform DFT and inverse DFT in time Onlogn. We used the sine series as it corresponds to the eigenvalue problem for Xx above.

Solved Determine The Half Range Fourier Series In The Range Chegg Com

The Fourier Transform in this case the 2D Fourier Transform is the series expansion of an image function over the 2D space domain in terms of cosine image orthonormal basis functions.

. The net area of the square wave from L to L is zero. Single shot predictions where the entire time series is predicted at once. The discrete implementation of the FFT maps a digital signal into its Fourier series coefficients or harmonics.

Fourier analysis is based on the idea that any time series can be decomposed into a sum of integral of harmonic waves of different frequencies. I used the for formula Ao 1. Almost half the information is redundant in standard and double-sided output formats.

Let us write fx as the sine series fx sum_n1infty b_n sin left fracn piLx right. Begingroup When I was learning about FTs for actual work in signal processing years ago I found R. However for Ao i got half of the answer.

Fourier saw that traditional marriage could potentially hurt womans rights as human beings and thus never married. The scipyfft module may look intimidating at first since there are many functions often with similar names and the documentation uses a. There are two rough approaches to this.

François Marie Charles Fourier. Hence theoretically we can employ a number of harmonic waves to generate any signal. This chapter introduces the frequency domain and covers Fourier series Fourier transform Fourier properties FFT windowing and spectrograms using Python examples.

Waveforms are not made up of a discrete number of frequencies but rather a continuous range of frequencies. Finally we use superposition to write the solution as. SciPy provides a mature implementation in its scipyfft module and in this tutorial youll learn how to use it.

INTRODUCTION TO FOURIER TRANSFORMS FOR IMAGE PROCESSING BASIS FUNCTIONS. A Fourier series ˈ f ʊr i eɪ-i ər is a sum that represents a periodic function as a sum of sine and cosine waves. A 0 0.

Fourier held that both men and women have a wide range of sexual needs and preferences which may change throughout their lives. The pulse option in the netlist line describing voltage source v1 instructs SPICE to simulate a square-shaped pulse waveform in this case one that is symmetrical equal time for each half-cycle and has a peak amplitude of 1 volt. Fast fourier transform FFT is one of the most useful tools and is widely used in the signal processing 12 14FFT results of each frame data are listed in figure 6From figure 6 it can be seen that the vibration frequencies are abundant and most of them are less than 5 kHz.

It is basically an average of fx in that range. 2004-present Laser Physics Letters doi. The Fourier series for an arbitrary function of time ft defined over the interval -T2 t T2 is.

Not as half the human couple. Fourier Series gives us a method of decomposing periodic functions into their sinusoidal components. Enter the upper integration limit the total range.

Nonumber That is we find the Fourier series of the odd periodic extension of fx. A_01Lint_-LLftdt a_n1Lint_-LLftcosn pi tLdt An even function has only cosine terms in its Fourier expansion. The second frequency will have a period half as long as the first twice the frequency.

The Fourier Series Grapher. Also the HSS-X point has greater values of amplitude than other points which corresponds with the. It requires that the range or length of the time series to be evaluated contains a total number of data points precisely equal to a 2-to-the-nth-power number eg.

The right half of the lower right image is not painted because it is the. Would be a good next step. The Fourier transform accomplishes this by breaking down the original time-based waveform into a series of sinusoidal terms each with a unique magnitude frequency and phase.

In a multi-step prediction the model needs to learn to predict a range of future values. L is half of the period of the function. This is clear from equations 5 6 and 7.

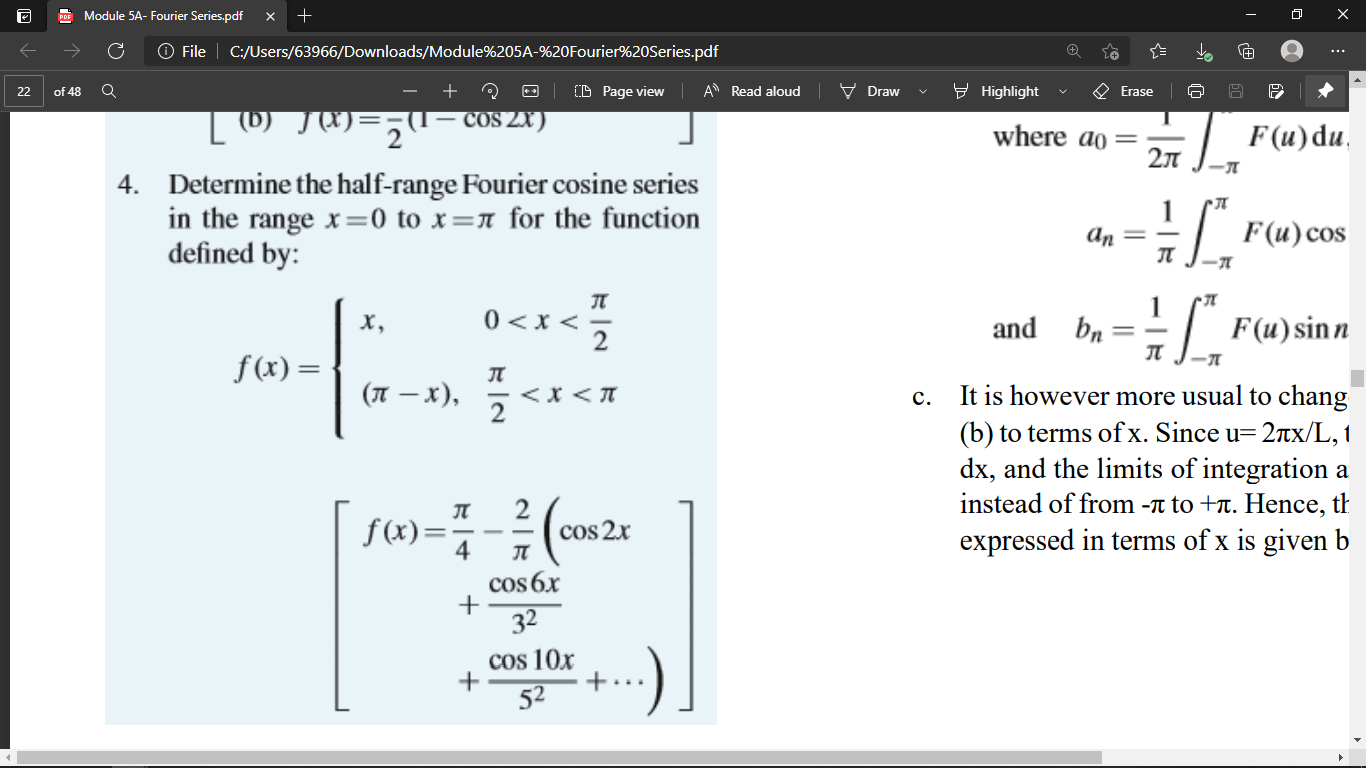
Hammings book Digital Filters and Bracewells The Fourier Transform and Its Applications good intros to the basics. If a function is defined over half the range say 0 to L instead of the full range from -L to L it may be expanded in a series of sine terms only or of cosine terms onlyThe series produced is then called a half range Fourier series. Presenting FFT results in this frequency range is a double-sided format as shown in Figure 7.

Fourier Series Calculator is a Fourier Series on line utility simply enter your function if piecewise introduces each of the parts and calculates the Fourier coefficients may also represent up to 20 coefficients. Looking at this sketch. First well plot the square wave to be analyzed.

Half Range Fourier Series. The Fourier transform is a powerful tool for analyzing signals and is used in everything from audio processing to image compression. Conversely the Fourier Series of an even or odd function can be analysed using the half range definition.

Do a discrete finite FT by hand of a pure tone signal over a few periods to get a feel for the. B_n 0 So we only need to calculate a 0 and a n when finding the Fourier Series expansion for an even function ft. The Fourier Transform is the.

So we know that. So for k 0 1 2 n-1 y y0 y1 y2 yn-1 is Discrete fourier Transformation DFT of given polynomial. The frequency of each wave in the sum or harmonic is an integer multiple of the periodic functions fundamental frequencyEach harmonics phase and amplitude can be determined using harmonic analysisA Fourier series may potentially contain an infinite.

A 0 a n and b n are coefficients that we need to calculate. So for the Fourier Series for an even function the coefficient b n has zero value. Thus unlike a single step model where only a single future point is predicted a multi-step model predicts a sequence of the future values.

Squarewave for SPICE Fourier analysis. One of the coolest side effects of learning about DSP and wireless communications is that you will also learn to think in the frequency domain. DFT DFT is evaluating values of polynomial at n complex nth roots of unity.

PlttitleTriangular wave signal analysis by Fouries series pltsavefigfs_triangularpng pltshow Example-4 Fourier series analysis for a sawtooth wave function User defined function import numpy as np import matplotlibpyplot as plt from scipyintegrate import simps L10 half wavelength Wavelength2L freq2 frequency.

Half Range Sine Cosine Fourier Series

Solved A Find The Half Range Fourier Cosine Series For The Chegg Com

Half Range Sine Cosine Fourier Series

Half Range Fourier Sine Cosine Series Solving Problems Youtube

Fourier Series Half Range Expansion Boundary Value Problems Lettherebemath Youtube

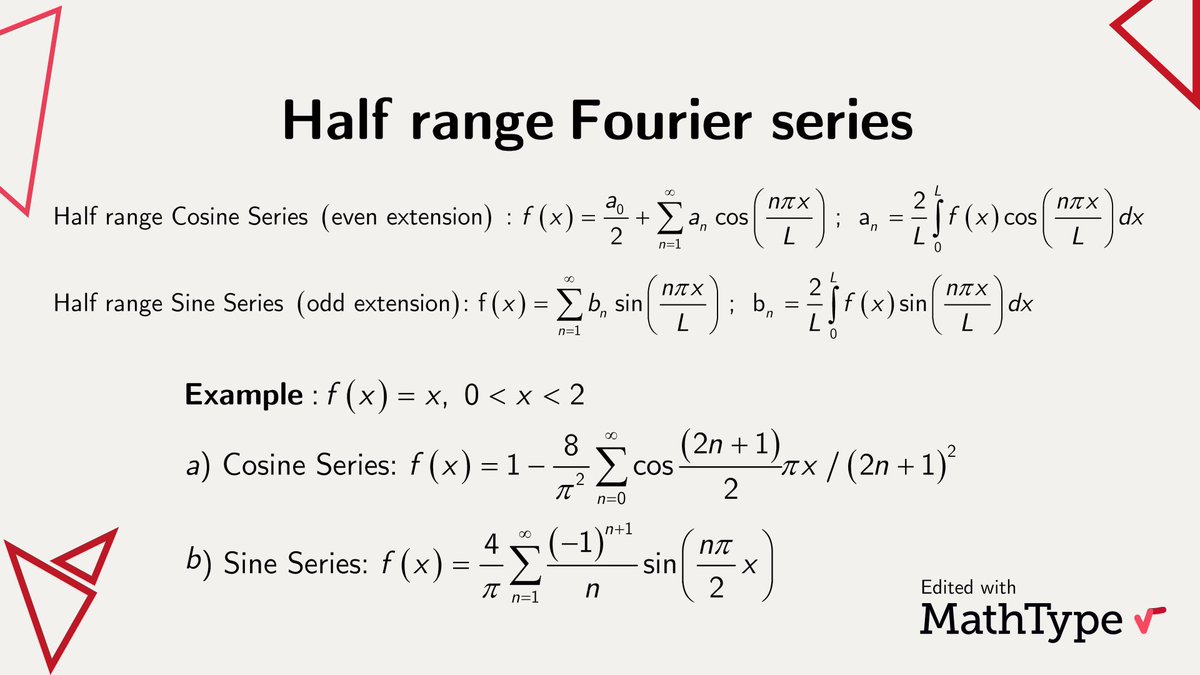
Mathtype On Twitter Did You Know About The Existence Of Half Range Fourierseries Well It Is Quite Interesting Take A Function F X On An Interval 0 L Then Two Different Extensions Of F